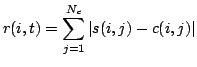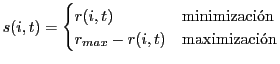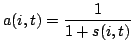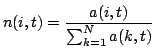7 Evaluación

Para el correcto funcionamiento de un Algoritmo Genético se debe de poseer un método que indique si los individuos de la población representan o no buenas soluciones al problema planteado. Por lo tanto para cada tipo de problema que se desee resolver deberá derivarse un nuevo método, al igual que ocurrirá con la propia codificación de los individuos.

De esto se encarga la función de evaluación, que establece una medida numérica de la bondad de una solución. Esta medida recibe el nombre de ajuste. En la naturaleza el ajuste (o adecuación) de un individuo puede considerarse como la probabilidad de que ese individuo sobreviva hasta la edad de reproducción y se reproduzca. Esta probabilidad deberá estar ponderada con el número de descendientes. Evidentemente no es lo mismo una probabilidad de reproducción del 25% en una población de un par de cientos de individuos que esa misma probabilidad en una población de varios millones.

En el mundo de los Algoritmos Genéticos se empleará esta medición para controlar la aplicación de los operadores genéticos. Es decir, permitirá controlar el número de selecciones, cruces, copias y mutaciones llevadas a cabo.

La aproximación más común consiste en crear explícitamente una medida de ajuste para cada individuo de la población. A cada uno de los individuos se les asigna un valor de ajuste escalar por medio de un procedimiento de evaluación bien definido. Tal y como se ha comentado, este procedimiento de evaluación será específico del dominio del problema en el que se aplica el Algoritmo Genético. También puede calcularse el ajuste mediante una manera 'co-evolutiva'. Por ejemplo, el ajuste de una estrategia de juego se determina aplicando esa estrategia contra la población entera (o en su defecto una muestra) de estrategias de oposición.

Se pueden diferenciar cuatro tipos de ajuste o fitness [Koza, 1992]:

• Fitness Puro: r(i,t)

  Es la medida de ajuste establecida en la terminología natural del propio problema. La ecuación 1 establece el cálculo del valor de bondad de un individuo i en un instante t (o generación).

  $$r(i,t) = \sum_{j=1}^{N_c} \vert s(i,j) - c(i,j) \vert$$ (1)

  
  
  $$\begin{multline*} Siendo: \\ s(i,j) = \text{valor deseado para el individuo \em... ...h{i} para el caso \emph{j}} \\ N_c = \text{Número de casos} \\ \end{multline*}$$
  
  

  Por ejemplo, supóngase una población de hormigas que deben llenar la despensa de cara al invierno. La bondad de cada hormiga será el número de piezas de comida llevadas por ella hasta el hormiguero.

  En los problemas de maximización, como sería el de las hormigas mencionado anteriormente, los individuos con un fitness puro elevado serán los más interesantes. Al contrario, en los problemas de minimización interesarán los individuos con un fitness puro reducido.

• Fitness Estandarizado: s(i,t)

  Para solucionar esta dualidad ante problemas de minimización o maximización se modifica el ajuste puro de acuerdo a la ecuación 2.

  $$s(i,t) = \begin{cases}r(i,t) & \text{maximización} \\ r_{max} - r(i,t) & \text{minización} \end{cases}$$ (2)

  
  

  En el caso de problemas de minimización se emplea directamente la medida de fitness puro. Si el problema es de maximización se resta de una cota superior $r_{max}$ del error el fitness puro. Empleando esta métrica la bondad de un individuo será mayor cuanto más cercano esté a cero el valor del ajuste. Por lo tanto, dentro de la generación t, un individuo i siempre será mejor que uno j si se verifica que $s(i,t) < s(j,t)$.

• Fitness Ajustado: a(i,t)

  Se obtiene aplicando la transformación reflejada en la ecuación 3 al fitness estandarizado.

  $$a(i,t) = \frac{1}{1+s(i,t)}$$ (3)

  
  

  De esta manera, el fitness ajustado tomará siempre valores del intervalo [0..1]. Cuando más se aproxime el fitness ajustado de un individuo a 1 mayor será su bondad.

• Fitness Normalizado: n(i,t)

  Los diferentes tipos de fitness vistos hasta ahora hacen referencia únicamente a la bondad del individuo en cuestión. El fitness normalizado introduce un nuevo aspecto: indica la bondad de una solución con respecto al resto de soluciones representadas en la población. Considerando una población de tamaño N, se obtiene según la ecuación 4.

  $$n(i,t) = \frac{a(i,t)}{\sum_{k=1}^{N}a(k,t)}$$ (4)

  
  

  Al igual que el fitness ajustado, siempre tomará valores del intervalo [0..1], con mejores individuos cuanto más próximo esté a la unidad. Pero a diferencia de antes, un valor cercano a 1 no sólo indica que ese individuo represente una buena solución al problema, sino que además es una solución destacadamente mejor que las proporcionadas por el resto de la población.

  La suma de los valores del fitness normalizado de todos los individuos de una población dará siempre 1.

  Este tipo de ajuste es empleado en la mayoría de los métodos de selección proporcionales al fitness.